Why You Should Always Call Even

Almost every game of ultimate starts with a flip to decide who pulls. Most players call even or odd seemingly on a whim, yet one of these choices is clearly better than the other. In this article I’ll show which choice is better, and why.

If the discs are perfectly fair – that is, they’re both 50% to be heads or tails – then even and odd are equally likely. But if the discs are skewed either way, they’re more likely to land even. I’m going to reveal the magic right away. This may not surprise you, but there is math behind it that I’m going to show you below. Ready? Okay. Here it the big disc flipping secret: Given that discs are not symmetrical on an up-down axis, they’re not equally likely to land heads or tails, so it’s better to call even.

Paul Illian wrote a great article about the flip way back in 2011. While he alluded to the math I’ll go over, he focused mostly on gathering empirical evidence about which way discs actually flip. I’m going to show that the correct choice is the same no matter what you believe about how likely a disc is to land either way.

The Math of the Flip

Okay, let’s dive into the math. I’ve noticed a strong correlation between ultimate prowess and advanced degrees in math and science, so for some of you this may be obvious. But if math is not your thing, don’t worry, it’s all fairly straightforward.

Let’s call the chance that the disc lands heads h and the chance it lands tails t. There are two ways to have the discs land even: two heads, or two tails. The chance of getting two heads is h*h which is the same thing as h2. The same is true for tails, and we add them together to get the chance of the discs being even:

Each disc has to land either heads or tails, which means in probabilistic terms that heads and tails have to sum to one. We can use this to say that t=1-h. Substituting into the above equation, we get:

Let’s graph it!

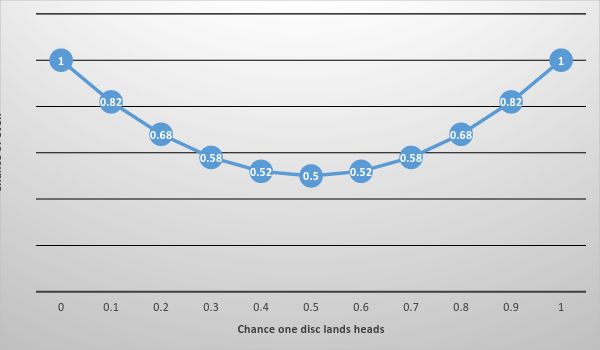
Notice that the graph bottoms out at .5. In other words, no matter what’s going on with the discs, by choosing even we guarantee ourselves at least a 50% chance of winning. And if the discs are skewed either way, we give ourselves a better chance by choosing even. In fact, the more skewed they are, the more likely even becomes. In game theory this is called a dominant strategy: even dominates odd because it has a significant upside and no downside.

Problems and Challenges

A key assumption that I didn’t state explicitly is that the chance of heads is the same for both discs. If you had two discs that skewed opposite directions – say, one that was 60% heads and one that was 40% heads – they’d actually be more likely to land odd.

I made that assumption because I believe the main reason for discs skewing one way or another is their unique shape, and all discs are basically the same shape (apart from surface imperfections). Ultimate players are notorious for rejecting any disc other than the Ultra-star model, even those that appear extremely similar.

Even if there are oddball discs out there, the above reasoning still holds as long as the discs are drawn randomly from the population. The only time a problem occurs is if you somehow know exactly one of the discs being used goes against the usual tendency. So, if you have a magical taco’d disc or a teammate with a bizarre flipping style, it might be better to call odd.

Conclusion

I’ve shown why you should always call even when you flip for the pull. There’s no downside to calling even and a very realistic upside. The edge you gain is likely to be small, but as ultimate becomes more and more competitive, every edge counts. Ultimate players may be odd, but more likely than not, the discs will land even.